No. 22

The childhood of algebraic geometry: the study of the geometry of cubic surfaces and their 27 lines. In 1849, Cayley and Salmon found that any smooth cubic surface contains 27 lines.
I produced the images below using the "cubic surface program xcsprg" (a prototype which is not available anymore) - the white line shown on the surfaces is the so-called parabolic line, i.e. the intersection of the surfaces with its hessian. The program was also used to produce a movie showing the deformation of a cubic surface containing an A₂ singularity together with the development of the 27 lines.

The Clebsch Cubic Surface containing 10 Eckardt points (where 3 lines meet):

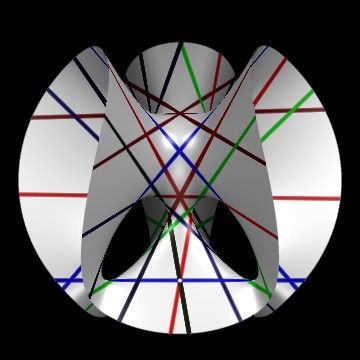
A general cubic surface containing 27 real lines. Note that each part of the (white) parabolic line touches three of the lines.

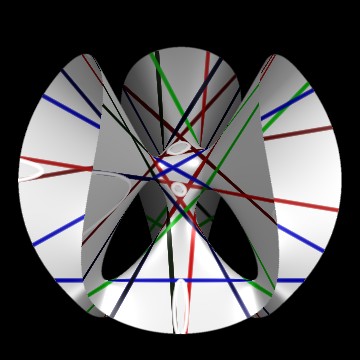
A double point develops:

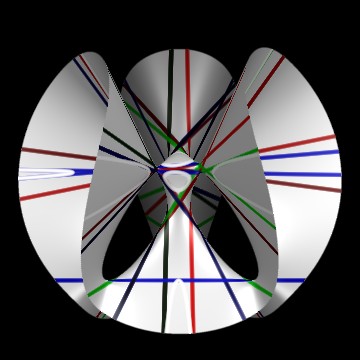
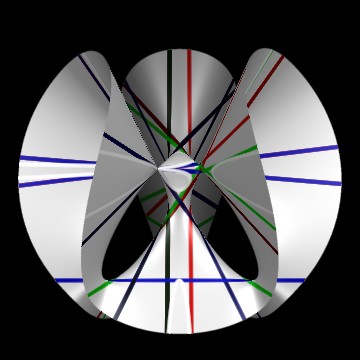
A cubic surface with a double point:

Back to the algebraic surface calendar.