I create very different kinds of mathematical objects, 2d, 3d, virtual, interactive. On this page, I give a brief overview on some of the kinds of objects I have created.
Mathematical Objects in Public

Larger numbers of my sculptures and/or visualizations are part of the permanent collections of the following institutions:
- University of Lisbon, Lisbon, Portugal (more than 70 of my sculptures are part of their collection),
- University of Strasbourg, Strasbourg, France (my complete series of 45 cubic surfaces with rational double points is part of their collection which is on display in their common room),
- Institute Henri Poincaré, Paris, France (more than 50 of my sculptures, plus math teaching tools, are part of their collection),
- University of Mainz, Mainz, Germany (more than 50 of my sculptures are part of their collection which is on display in the department of mathematics),
- University of Marburg, Marburg, Germany (more than 25 of my sculptures, mainly from algebraic geometry or differential geometry; some of them are on display in the math library),
- Experiminta Science Center, Frankfurt, Germany (more than 10 of my sculptures and laser-in-glass objects are on display in the exhibition),
- Deutsches Museum München, Munich, Germany (both three of my visualizations of algebraic geometry and the Surfer program (containing many of my texts and equations which are illustrated interactively) is part of the permanent collection).
Other institutions who purchased several of my math objects include:
- the Mathematische Forschungsinstitut Oberwolfach (MFO), Oberwolfach, Germany (here, you may even purchase some of my mathematical laser-in-glass objects; for many others, please, contact me),
- the Mathematical Sciences Research Institute (MSRI), Berkeley, USA,
- the Freudenthal Institute for Science and Mathematics Education at Utrecht, the Netherlands.
Mathematical Sculptures

I create highest quality mathematical sculptures. Often, these are produced using 3d-printers such as the three shown in the photo above. My mathematical objects are based on a large number of different mathematical subjects. I always use the best available materials for each particular mathematical object by choosing the perfect producer for each of my objects, both with respect to quality and price.
- See math-sculpture.com for my online catalogue of my math sculpture designs.
- See MO-Labs.com for general information and news about my math object business.
Math in Glass

Laser-in-glass is a perfectly suited technique to create top quality math objects in glass. My mathematical sculptures in glass are based on a large number of different mathematical subjects. I always use the best available materials for each particular mathematical object by choosing the perfect producer for each of my objects, both with respect to quality and price. Laser-in-glass makes a great fit for highly fragile shapes such as the world record surface with many singularities shown above.
- See mathe-in-glas.de (in German) for a small selection of my portfolio of laser in glass objects.
- See MO-Labs.com for general information and news about my math object business.
Mathematical Jewelry

Each of my math jewelry is a miniature sculpture on its own. Some of my designs are classics in mathematical design. But on the other hand, you will see that many of my designs are unique worldwide – you will not see anything similar anywhere in the world.
E.g., I designed the first complete series of so-called cubic surface models in 2012 – and for each of them, I can create a very special pendant for you! Just contact me! Some are already available via my online catalogue, see:
Mathematical Images and Animations

The images I create may be used at diverse locations:
- at science museums: e.g., the image of my “septic surface with 99 singularities” shown above tours around the world with the math exhibition “Imaginary” since 2008; three other visualizations are part of the permanent collection of the “Deutsches Museum München” at Munich, Germany,
- at home: museum quality prints are available for most of my high quality math visualizations; just contact me,
- at school or at the university: some of my images are not ment to look astonishingly beautiful, but just to explain a mathematical phenomenon,
- in or on covers of publications: Quite a few of my visualizations have appeared in or as covers of books, journals, or other printed products. Indeed, my first math visualization job for a paying client were some of the SuSE linux covers, see: http://oliverlabs.net/suse/.
Mathematical Models for Teaching

Many of my models may be used in teaching at the university level. E.g., our cubic surface models are interesting tools for a more visual algebraic geometry or topology course.
But I have also created quite a few objects which bring a lot of fun even for kids in primary school such as my soap water experimental minimal surface 3d-printed tools.
Other objects are intended for college level, such as the graphs of functions in two variables within a coordinate frame.
Mathematical Interactive Illustrations
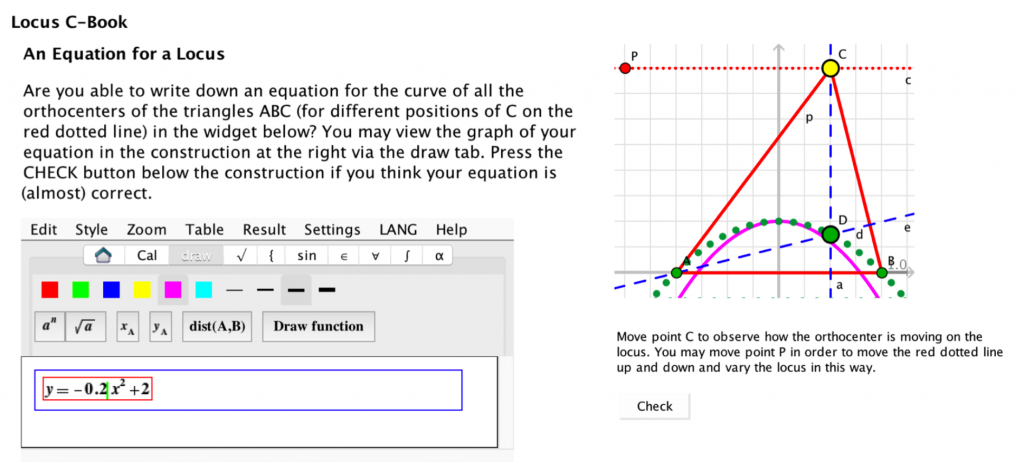
Over the years, I created lots of interactive illustrations, mainly for research and/or teaching purposes. I even taught about dynamic geometry software several times at different universities.
From 2014-2016, I was working in the EU project called “MC Squared” (mathematical creativity squared) on the extension and usage of an educational framework for e-learning of mathematics which aims to support creativity both on the side of the author/teacher of math material, and on the side of its user/student/school kid. One of the ideas that extended drastically the opportunities reachable with an acceptable amount of work was “cross-widget-communication”, i.e. communication between widgets of very diverse backgrounds within the system. A brief article on this in German is linked here: article on cross widget communication (2016, with U. Kortenkamp, in German).
Math Software
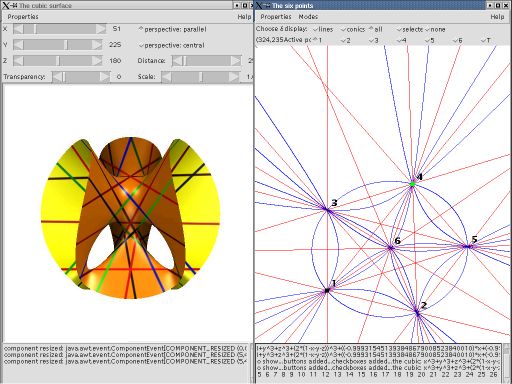
- The screenshot above shows one of my very first visualization tools; I developed this prototype software (called “xcsprg”) in 2001 when I wrote my diploma thesis on “cubic surfaces”. It was the very first interactive software providing a real-time visualization of a large space of cubic surfaces.
- “spicy” prototype software (2001), a first prototypical dynamic geometry software connected to a 2d and 3d algebraic curve and surface visualizer; this was before GeoGebra existed,
link to my related article: A visual introduction to cubic surfaces using the computer software spicy (with D. van Straten, 2002). - “surfex” prototype software (2001), a first prototypical software for the comfortable interactive visualization of algebraic surfaces,
link to my related article: Illustrating the classification of real cubic surfaces (with Stephan Holzer, 2006). - “Surfer” software (the concept is based on my software “surfex”; but it was completely developed from scratch by the MFO as a tool for math exhibitions, 2008), used in more than 100 exhibitions worldwide, either in the original or a more recent version which has been developped later without me.
- “MindCurver“: A game to get a first idea of implicit equations for algebraic plane curves. This game is playable for school kids starting roughly at the age of 15. See: www.OliverLabs.net/MindCurver/
