Most of my research is on algebra, geometry, history, or their interactions, often related to computers in one way or another:
- history of caustics
- history of algebraic geometry in the 19th century
- mathematical models and sculptures – their history and mathematics,
- geometrical modelling, in particular of non-linear surfaces,
- (hyper-) surfaces with many singularities,
- computational algebraic geometry and computer algebra,
- e-learning software tools for mathematics,
- didactics of mathematics – geometry, algebra, 3d-printing for teaching, using 3d-models in teaching.
Some of my research is listed on researchgate.net.
Some Milestones of my Research
History of Mathematics and Mathematical 3d-Models

- 2017: Straight lines on models of curved surfaces. In: The Mathematical Intelligencer, Springer, see the article online.
- 2015: On Alfred Clebsch and Cubic Surfaces, p. 2798-2800 in: Oberwolfach report No. 47/2015 (PDF).
- 2014: Faszinierende Mathematik. Singuläre Flächen in Glas. In: D. Ludwig, C. Weber, O. Zauzig: Das materielle Modell, Wilhelm Fink.
Didactics of Mathematics and E-Learning
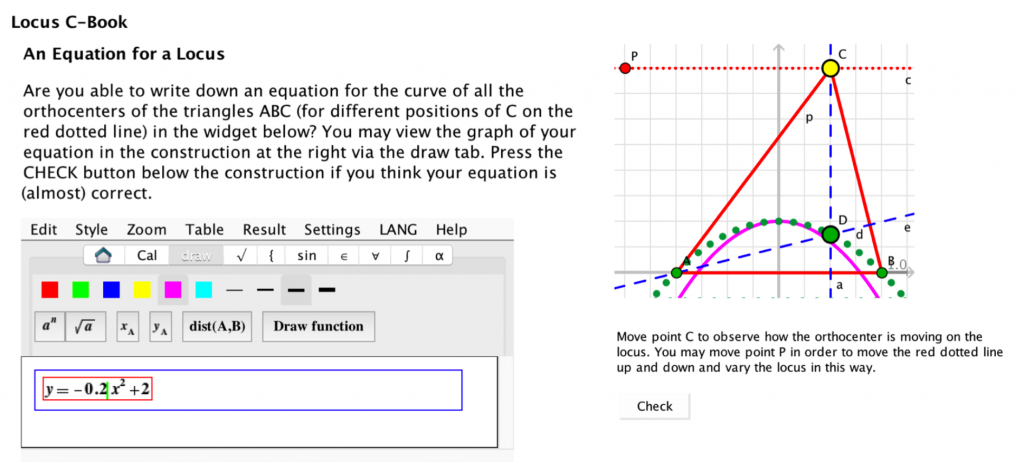
- 2018 (with S. Halverscheid): Felix Klein’s Mathematical Heritage seen through 3d Models. In: The Legacy of Felix Klein, pp. 131-152, Springer.
- 2016 (with S. Karkalas and M. Mavrikis): Towards analytics for educational interactive e-Books: The case of the reflective designer analytics platform (RDAP), in: Proceeding LAK ’16 Proceedings of the Sixth International Conference on Learning Analytics & Knowledge (see article on the web)
- 2016 (with M. El-Demerdash, J. Trgalova, J.-F. Nicaud): Collaborative Design of Educational Digital Resources for Promoting Creative Mathematical Thinking, conference paper for the “International Congress of Mathematical Education”, in: ICME 13 Proceedings (pdf)
- 2016 (with U. Kortenkamp): Bausteine in digitalen Lernumgebungen vernetzen: Technologie zur Gestaltung und Analyse von kreativen Lernprozessen, in: Proceedings of the GDM Tagung 2016 (pdf)
- 2011: Terme in Bildern (20 Seiten), in: Tagungsband des GDM-Arbeitskreises Geometrie.
Applications of Mathematics

- 2011 (with G. Barczik and D. Lordick): Algebraic Expansions: Broadening the Scope of Architectural Design through Algebraic Surfaces
in: Computational Design Modelling: Proceedings of the Design Modelling Symposium Berlin 2011 - 2009 (with G. Barczik and D. Lordick): Algebraic Geometry in Architectural Design. In: Proceedings of the 27th eCAADe, Istanbul, Turkey.
- 2009: A List of Challenges for Real Algebraic Plane Curve Visualization Software, p. 137-164 in: Nonlinear Computational Geometry, edited by I. Emiris and F. Sottile and T. Theobald, IMA Volume 151, Springer.Downloads: Article as PDF. Explicit list of polynomials for challenges in low degrees.
Pure Mathematics (Algebra and Geometry)

- 2007 (with Hans-Christian Graf von Bothmer, Josef Schicho, Christiaan van de Woestijne): The Casas-Alvero conjecture for infinitely many degrees, (see also: arxiv.org/math.AC/0605090), p. 224-230 in: J. Algebra, Vol. 316, No 1.
- 2006: A Septic with 99 real Nodes, (see also: arxiv.org/math.AG/0409348), p. 299-313 in: Rend. Sem. Mat. Univ. Pad., Vol. 116.
- 2005: Hypersurfaces with many singularities – History, Constructions, Algorithms, Visualization. Ph. D. thesis, Mainz, Germany.
Mathematical Software
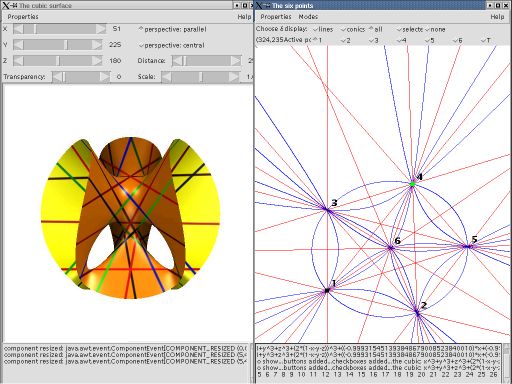
- 2014-16: several publications within the European project Mathematical Creativity Squared, in particular I was the deliverable manager of three so-called widget catalogues (written with other team members), see the website of the MC2 project
- 2006 (with S. Holzer): Illustrating the Classification of Real Cubic Surfaces, p. 119-134 in: M. Elkhadi, B. Mourrain, R. Piene, Algebraic Geometry and Geometric Modelling (Springer).
- 2002 (with D. van Straten): A Visual Introduction to Cubic Surfaces using SPICY, in: M. Joswig, N. Takayama: Algebra, Geometry and Software Systems (Springer).
